Наглядное пересечение N-1 пространства N-мерным объектом, или «Теперь я повидал всё»!
Андрей Свирский - 5-03-2017
Строим 3D проекты – Шаг 4

Гиперкуб призывает идти дальше 3D
Продолжим изучение основ низкоуровневого WebGL и усовершенствуем тестовую программу. Установим 3D движение за счет заметного изменения положения точек по оси Z в модели программы.
Анимация
Движение объекта, особенно вращение, позволяет понять его свойства, в частности, является ли он трехмерным.
Чтобы увидеть изменения положения объекта по оси Z, мы должны посмотреть на движение из точечной камеры. Для этого необходимо задать расположение камеры.
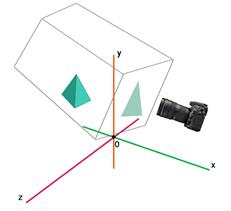
Изначально объект находится в центре координат, а объектив камеры – перпендикулярно плоскости XY. При этом, можно сказать, что объектив расфокусирован (вся моделируемая область прямоугольно проецируется на матрицу, равную размеру этой области). Это модельные координаты:
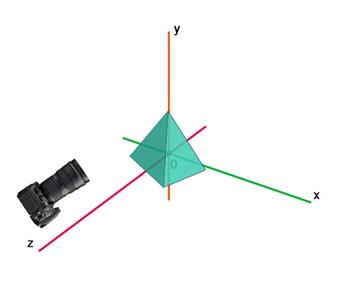
Модельные координаты
При переходе в мировые координаты, камера располагается в центре координат:
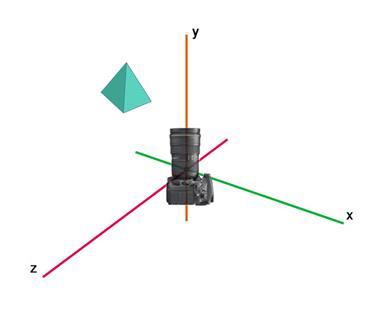
Мировые координаты
При переходе в видовые координаты, объектив камеры смотрит на объект:
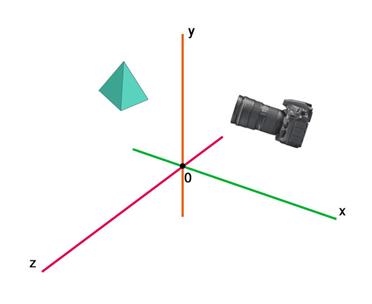
Видовые координаты
Для преобразования координат XYZ их удобно записать в виде матрицы. Процесс трансформации матрицы координат из модельных в видовые, и далее в проекцию на экран называется модель-вид проекция, МВП (Model-View-Projection, MVP).
Проекция на экран может быть ортогональной или перспективной:
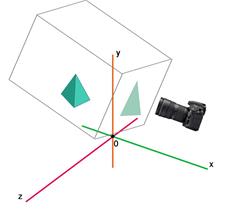
Ортогональная проекция на экран
Перспективная проекция на экран
Для работы с матрицами координат лучше подключить библиотеку gl-matrix.js (скачать тут github.com/toji/gl-matrix). Скачиваем, подключаем в шапке программы:
<script src="js_std/gl-matrix-min.js"></script>
Фактически, данная библиотека gl-matrix — это целый фреймворк для работы с матрицами. Она позволяет выполнять операции со следующими объектами:
* 2,3,4-мерными векторами – vec2, vec3, vec4;
* матрицами 2×2, 3×3, 4×4 – mat2, mat3, mat4;
* кватернионами – quat4.
С матрицами выполняются операции следующего рода:
копия, сложение, вычитание, умножение,
умножение на скаляр, на вектор,
векторное, скалярное произведение,
присвоение обратного знака элементам,
создание единичного вектора такого же направления,
создание единичного вектора, указывающего на другой вектор,
вычисление длины вектора,
нормализация вектора,
вычисление детерминанта,
вычисление инверсной матрицы,
преобразование вектора по матрице,
создание единичной матрицы,
транспонирование (отражение относительно диагонали),
конвертация в матрицу более высокой размерности,
трансформирование,
параллельный перенос,
поворот матрицы на угол вокруг оси,
создание усеченной матрицы,
евклидово расстояние между двумя векторами,
линейная интерполяция между двумя векторами,
сферическая линейная интерполяция между двумя кватернионами,
проекция из видовых координат в модельные,
перспективная, ортогональная проекция,
создание видовой матрицы с заданием точки обзора, фокальной точки, верхней оси
создание кватерниона вращения между двумя нормализованными векторами,
создание матрицы из кватерниона вращения и вектора преобразования,
создание кватерниона из матрицы вращения,
вычисление координаты W кватерниона из XYZ,
вычисление сопряжения,
вычисление матрицы по кватерниону,
сохранение угла и оси в 4-мерном векторе, где XYZ задают ось, а W это угол в радианах,
возврат матрицы в виде строки.
То есть, нечаянно, мы рискуем вспомнить или понять то, чему нас учили на высшей математике 🙂
Подготовка программы к 3D анимации.
Заведем две новые переменные для хранения матриц модель-вид и проекции.
var mvMatrix = mat4.create(); //To store our model-view and projection matrices.
var pMatrix = mat4.create();
И заведем в вершинном шейдере две униформы для приёма данных этих матриц:
<script id="shader-vs" type="x-shader/x-vertex">
attribute vec3 aVertexPosition;
attribute vec3 aVertexColor;
uniform mat4 uMVMatrix;
uniform mat4 uPMatrix;
varying highp vec4 vColor;
void main(void)
{
//gl_Position = vec4(aVertexPosition, 1.0);
gl_Position = uPMatrix * uMVMatrix * vec4(aVertexPosition, 1.0);
vColor = vec4(aVertexColor, 1.0);
}
</script>
Переменная с идентификатором uniform (униформа) – глобальная GLSL переменная для передачи параметров в шейдер, которая не меняется для всех элементов примитива-объекта.
Теперь, каждая вершина vec4 (aVertexPosition, 1.0) в пространстве будет проецироваться на экран умножением произведения матриц на вектор uPMatrix * uMVMatrix * vec4 (умножение некоммутативно, то есть важен порядок умножения именно в такой последовательности) .
Для установки наших двух матриц mvMatrix и pMatrix, перепишем функцию setupWebGL:
function setupWebGL()
{
//The default value to set the color buffer.
gl.clearColor(0, 0.5, 0.5, 1);
gl.clear(gl.COLOR_BUFFER_BIT);
gl.viewport(0, 0, canvas.width, canvas.height);
mat4.identity(mvMatrix);
mat4.translate(mvMatrix, [0, 0, -2.0]);
mat4.rotate(mvMatrix, 0.50, [1.0, 0.0, 0.0]);
mat4.rotate(mvMatrix, -0.50, [0.0, 1.0, 0.0]);
mat4.perspective(45, canvas.width / canvas.height, 0.1, 100.0, pMatrix);
}
gl.viewport устанавливает рабочую область части canvas, в которую будет выводится графика нашей программы. В данном случае мы выставили всю canvas.
Для mvMatrix в identity мы создаем единичную матрицу. В translate мы смещаем ее по оси Z умножением матрицы на вектор [0, 0, -2.0]. А в rotate поворачиваем относительно оси X на 0.5, а относительно оси Y на -0.5.
Для pMatrix в perspective мы задали для рабочей области угол обзора, соотношение ширины и высоты, переднюю и заднюю границы пространства, в котором помещается модель.
Далее, нам необходимо связать наши матрицы mvMatrix и pMatrix в JavaScript с униформами uPMatrix и uMVMatrix в шейдере. Для этого добавим в конец программы функцию getMatrixUniforms:
function getMatrixUniforms()
{
glProgram.mvMatrixUniform = gl.getUniformLocation(glProgram, "uMVMatrix");
glProgram.pMatrixUniform = gl.getUniformLocation(glProgram, "uPMatrix");
}
После отработки getMatrixUniforms для отправки матриц в шейдер, будем использовать еще одну функцию — setMatrixUniforms, ее тоже добавим в конец программы:
function setMatrixUniforms()
{
gl.uniformMatrix4fv( glProgram.mvMatrixUniform, false, mvMatrix);
gl.uniformMatrix4fv( glProgram.pMatrixUniform, false, pMatrix);
}
Настройка программы.
Все приготовления для работы с матрицами преобразования координат сделаны. Теперь перепишем основной цикл:
if(gl)
{
initShaders(); //[2]
setupBuffers(); //[3].1
getMatrixUniforms();
(function animLoop()
{
setupWebGL(); //[1]
setupDynamicBuffers(); //[3].2
setMatrixUniforms();
drawScene(); //[4]
requestAnimationFrame( animLoop, canvas);
})();
}
И будем теперь менять в цикле программы координату Z каждой вершины в setupDynamicBuffers:
//3D-Move.
var triangleVertices =
[
//Triangle's points coodinates.
-0.5 , 0.5, -0.5 + x_delta,
0.0 , 0.0, -0.5 + x_delta,
-0.5 , -0.5, -0.5 + x_delta
];
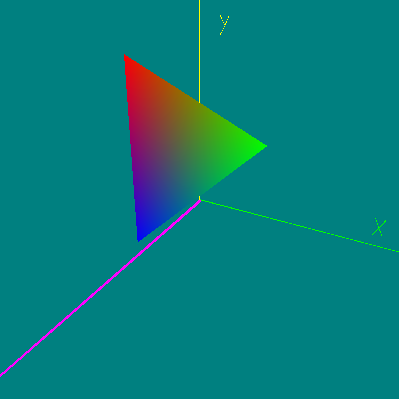
Движение примитива в 3D
Для наглядности можно еще добавить оси координат на нашу модель до прорисовки треугольника (как изображено выше). Мы не видим, как треугольник пересекает оси координат, потому что нет теста глубины, и поэтому наверху всегда оказывается объект, нарисованный последним.
Наша камера теперь в виде точки в пространстве, поэтому мы различаем приближение и удаление треугольника-примитива.
На следующем шаге мы планируем нарисовать объемную фигуру, сделать динамическое вращение, добавить тест глубины для прорисовки только видимой части.
 CogITas
CogITas