Луч света заметен в темноте
Андрей Свирский - 12-04-2017
Строим 3D проекты – Шаг 9

Реализм света и отражений
До настоящего момента мы работали с объектами в равномерном окружающем свете. Теперь рассмотрим направленные источники света и отражение света от объектов при этом. Направленный свет делает объект более реалистичным и трехмерным.
Виды источников света и отражений:

Окружающий свет (ОС). Равномерный.
|

Отражение окружающего света (ОО). От ОС. Матовое. |

Направленный свет (НС). От очень далеких источников, например, от солнца или луны.
|

Рассеянное отражение (РО) и зеркальное отражение (ЗО).
|

Точечный свет (ТС). От близкого источника, например, от лампочки. |
|
Точечный свет направленный (ТСН). Сформированный светильником. |
|

Сумма трех видов отражений |
|
По умолчанию мы работали с ОО в ОС. Теперь сделаем для начала РО в НС. Должен получиться примерно такой результат:

Окружающее и рассеянное отражение
Отражение в окружающем свете
Настроим сначала по-другому ОО в ОС. Подключим буфер для цвета, как в шаге 5, чтобы цвет при отключенной текстуре передавался в шейдеры из программы JS таким образом:
<script id="shader-vs-09pr" type="x-shader/x-vertex">
varying highp vec4 vColor09pr;
…
vColor09pr = vec4(aVertexColor09pr, 1.0);
</script>
<script id="shader-fs-09pr" type="x-shader/x-fragment">
varying highp vec4 vColor09pr;
…
//Было так: gl_FragColor = vec4(1.0, 0.1, 0.1, 1.0); //Red.
gl_FragColor = vec4(vColor09pr.xyz, vColor09pr.a);
</script>
Включаем переменные для буфера и отправки буфера в шейдер:
//Colors.
var trianglesColorBuffer09pr = null;
var vertexColorAttribute09pr = null;
Задаем цвета для вершин. Все цвета делаем одинаковые, чтобы потом лучше были видны эффекты от освещения:
function setupBuffers09pr()
{
var triangleVerticeColors = [];
…
for(var i=0; i<VertexIndices.length; ++i) //0 to 60
{
…
//Color of vertice. -----------------------------
triangleVerticeColors.push (0.8); //R
triangleVerticeColors.push (0.1); //G
triangleVerticeColors.push (0.1); //B
}
…
//Color.
trianglesColorBuffer09pr = gl09pr.createBuffer();
gl09pr.bindBuffer (gl09pr.ARRAY_BUFFER, trianglesColorBuffer09pr);
gl09pr.bufferData (gl09pr.ARRAY_BUFFER, new Float32Array (triangleVerticeColors), gl09pr.STATIC_DRAW );
}
Отправляем цвета в шейдеры:
function MoveStaticDataInShader09pr()
{
//Move data into shader.
…
//Color
vertexColorAttribute09pr = gl09pr.getAttribLocation (glProgram09pr, "aVertexColor09pr");
gl09pr.enableVertexAttribArray (vertexColorAttribute09pr);
gl09pr.bindBuffer (gl09pr.ARRAY_BUFFER, trianglesColorBuffer09pr);
gl09pr.vertexAttribPointer (vertexColorAttribute09pr, 3, gl09pr.FLOAT, false, 0, 0);
}
Смотрим результат, он такой же, как и был раньше:

Отражение в идеальном окружающем свете
Теперь переходим к РО в НС
Рассеянное отражение (РО) и зеркальное отражение (ЗО) зависят от угла падения света, поэтому необходимо определить лицевую сторону каждой поверхности. Это делается с помощью вычисления нормального вектора N к поверхности (нормальный — перпендикулярный к поверхности):
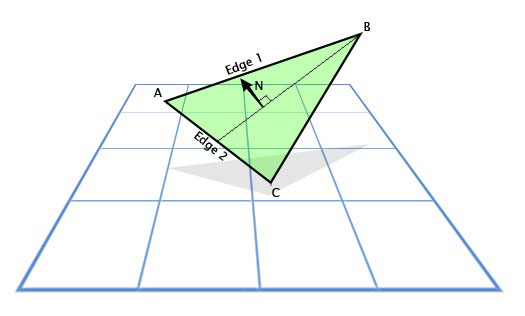
Нормаль к поверхности
Основное выражение освещённости записывается как скалярное произведение N • L, где N — это нормаль к освещаемой поверхности, а L — это нормализованный вектор направления света. В результате поверхность выглядит яркой, когда на неё прямо падает свет, и тёмной, когда этого не происходит.
Нам понадобится преобразование длины вектора в равную единице – нормализация вектора (мы просто делим каждый компонент вектора на длину вектора):
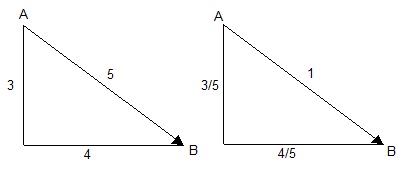
Нормализация вектора
На такой вектор удобно умножать – он не искажает сомножитель.
Сначала создадим шейдеры. Начнем с финального действия программы, то есть с пиксельного шейдера.
<script id="shader-fs-09pr" type="x-shader/x-fragment">
varying highp vec3 vLight09pr;
…
else
{
//gl_FragColor = vec4(0.8, 0.1, 0.1, 1.0); //RED
//gl_FragColor = vec4(vColor09pr.xyz, vColor09pr.a); //No light.
gl_FragColor = vec4(vColor09pr.xyz * vLight09pr, vColor09pr.a);
}
}
</script>
Мы умножили вектор цвета на вектор света. Вектор света мы вычисляем в вершинном шейдере:
<script id="shader-vs-09pr" type="x-shader/x-vertex">
…
//Light.
attribute vec3 aVertexNormal09pr;
uniform mat3 uConvertNormalMatrix09pr;
varying highp vec3 vLight09pr;
void main(void)
{
…
//Light.
//Ambient.
vec3 ambientLight = vec3(0.5, 0.5, 0.5);
//Diffuse.
vec3 diffuseLightColor = vec3(0.5, 0.5, 0.5);
//1st step - vector L, length = 1.
vec3 directionalLightPosition = normalize( vec3(10.0, 10.0, 5.0) );
//2nd step - vector N.
vec3 transformedNormal = uConvertNormalMatrix09pr * aVertexNormal09pr;
//3rd step.
float diffuseLightAmount = max( dot( transformedNormal, directionalLightPosition), 0.0);
//Out.
//1 variant - Ambient.
//vLight09pr = ambientLight;
//2 variant - Diffuse.
//vLight09pr = diffuseLightAmount * diffuseLightColor;
//3 variant - Ambient + diffuse.
vLight09pr = ambientLight + (diffuseLightAmount * diffuseLightColor);
}
</script>
Определение степени рассеяния света требует непростого комментария:
- Для установки направления света directionalLightPosition мы задали вектор и нормализовали его к единичному.
- Для установки направления нормали (преобразования нормали к модельным координатам) в transformedNormal мы поместили произведение инверсной транспонированной матрицы модельных координат uConvertNormalMatrix09pr и матрицы нормалей aVertexNormal09pr.
- Наконец, для подсчета степени РО diffuseLightAmount мы взяли сонаправленные относительно поверхности вектора нормали и света (неотрицательное значение скалярного произведения (dot) этих векторов).
Суть скалярного произведения векторов ясна из картинки:
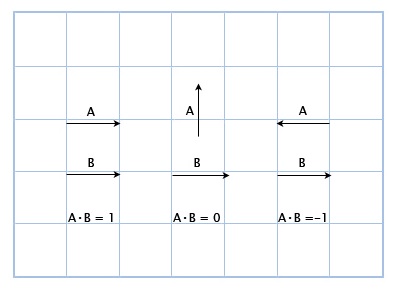
Практическое применение скалярного произведения векторов
Здесь мы можем увидеть, что если вектора указывают в одном направлении, то их скалярное произведение больше нуля.
Когда они перпендикулярны друг другу, то скалярное произведение равно нулю.
И когда они указывают в противоположных направлениях, их скалярное произведение меньше нуля.
Теперь нам осталось в программе JS задать входные данные вершинного шейдера – матрицы нормалей aVertexNormal09pr и матрицы преобразования этих нормалей в проекцию МВП uConvertNormalMatrix09pr.
Добавляем переменные для хранения буфера нормальных векторов, его передачи в шейдер и матрицы их преобразования в проекцию МВП.
//Light.
var trianglesNormalBuffer09pr = null;
var vertexNormalAttribute09pr = null;
var ConvertNormalMatrix09pr = mat3.create();
В setupWebGL мы делаем инверсную матрицу ConvertNormalMatrix09pr (при умножении на которую исходная матрица даёт в результате единичную матрицу) из матрицы модельных координат mvMatrix09pr:
mat4.toInverseMat3 (mvMatrix09pr, ConvertNormalMatrix09pr);
mat3.transpose (ConvertNormalMatrix09pr);
Единичная матрица — квадратная матрица, элементы главной диагонали которой равны единице, а остальные равны нулю.
Матрица ConvertNormalMatrix09pr должна быть 3×3. Поэтому мы берем верхнюю часть матрицы mvMatrix09pr и вычисляем транспонированную матрицу (замена строк на столбцы).
Включаем поиск униформы для матрицы преобразования:
function getMatrixUniforms()
{
…
glProgram09pr.normalMatrixUniform = gl09pr.getUniformLocation (glProgram09pr, "uConvertNormalMatrix09pr");
}
и готовимся передавать в униформу вычисленную матрицу преобразования ConvertNormalMatrix09pr:
function setMatrixUniforms()
{
…
gl09pr.uniformMatrix3fv (glProgram09pr.normalMatrixUniform, false, ConvertNormalMatrix09pr);
}
Теперь к вычислению нормалей. Мы используем две грани каждого треугольника в качестве пересекающихся векторов:
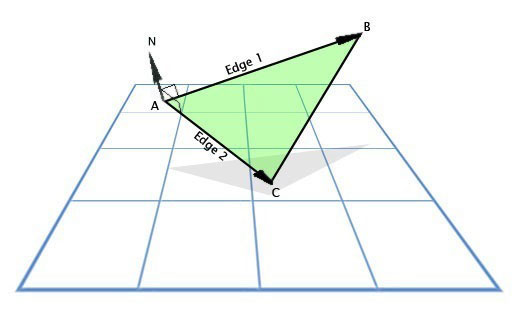
Нормаль к векторам и поверхности
Сначала вычисляем координаты двух граней, и для определения перпендикулярного к ним вектора-нормали вычисляем векторное произведение этих граней.
Результат векторного произведения двух векторов – это вектор-нормаль, перпендикулярный обоим векторам и содержащей их плоскости:
w = cross (u, v);
[w.x = u.Y * v.Z - u.Z * v.Y;
w.y = u.Z * v.X - u.X * v.Z;
w.z = u.X * v.Y - u.Y * v.X;]
Вставляем в setupBuffers09pr () вычисление нормалей для каждого треугольника:
var triangleNormals = [];
//20 triangles - normal will be the same for each vertex of triangle
for(var i=0; i<VertexIndices.length; i+=3)
{
var a = VertexIndices[i]; //1st triangle's point.
var b = VertexIndices[i + 1]; //2nd triangle's point.
var c = VertexIndices[i + 2]; //3rd triangle's point.
//1st side (a-b) of triangle.
var v1 = [
triangleVerticesOriginal[ a*3] - triangleVerticesOriginal[ b*3],
triangleVerticesOriginal[ a*3 + 1] - triangleVerticesOriginal[ b*3 + 1],
triangleVerticesOriginal[ a*3 + 2] - triangleVerticesOriginal[ b*3 + 2],
];
//2nd side (a-c) of triangle.
var v2 = [
triangleVerticesOriginal[ a*3] - triangleVerticesOriginal[ c*3],
triangleVerticesOriginal[ a*3 + 1] - triangleVerticesOriginal[ c*3 + 1],
triangleVerticesOriginal[ a*3 + 2] - triangleVerticesOriginal[ c*3 + 2],
];
//Count normal - the cross-product of two sides.
//[w.x = u.Y * v.Z - u.Z * v.Y;
// w.y = u.Z * v.X - u.X * v.Z;
// w.z = u.X * v.Y - u.Y * v.X;]
var cross = [
v1[1]*v2[2] - v1[2]*v2[1],
v1[2]*v2[0] - v1[0]*v2[2],
v1[0]*v2[1] - v1[1]*v2[0],
];
//Push in array same value for each of the three vertices.
triangleNormals.push.apply (triangleNormals, cross);
triangleNormals.push.apply (triangleNormals, cross);
triangleNormals.push.apply (triangleNormals, cross);
}
trianglesNormalsBuffer09pr = gl09pr.createBuffer();
gl09pr.bindBuffer (gl09pr.ARRAY_BUFFER, trianglesNormalsBuffer09pr);
gl09pr.bufferData (gl09pr.ARRAY_BUFFER, new Float32Array (triangleNormals), gl09pr.STATIC_DRAW);
Передаем буфер нормалей в шейдер:
function MoveStaticDataInShader09pr()
{
…
//Light.
vertexNormalAttribute09pr = gl09pr.getAttribLocation (glProgram09pr, "aVertexNormal09pr");
gl09pr.enableVertexAttribArray (vertexNormalAttribute09pr);
gl09pr.bindBuffer (gl09pr.ARRAY_BUFFER, trianglesNormalBuffer09pr);
gl09pr.vertexAttribPointer (vertexNormalAttribute09pr, 3, gl09pr.FLOAT, false, 0, 0);
}
В результате, пока что видим отдельные треугольники фигуры:

Отрицательные нормали дают свет с обратной стороны
Проблема в разном направлении обхода вершин треугольников: одни – по часовой стрелке, другие – против. Чтобы нормали были направлены в одном направлении, необходимо, чтобы обход вершин был везде одинаковым, например, против часовой стрелки. Поменяем порядок части треугольников:
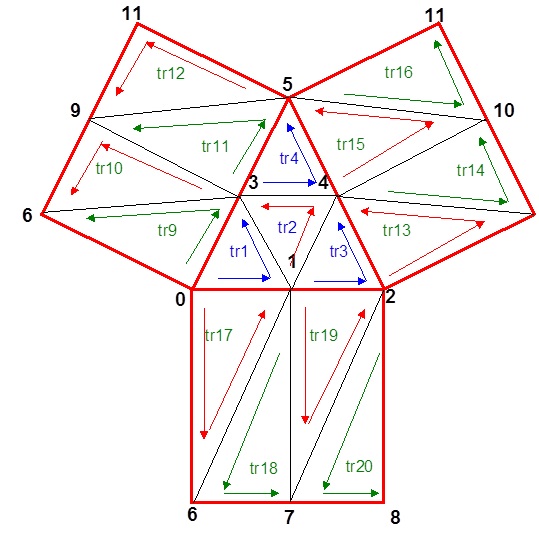
Направление обхода вершин
VertexIndices =
[
//front face
0,1,3, //tr1
1,4,3, //tr2
1,2,4, //tr3
3,4,5, //tr4
//rear face
6,7,9, //tr5
7,10,9, //tr6
7,8,10, //tr7
9,10,11, //tr8
//left side
0,3,6, //tr9
3,9,6, //tr10
3,5,9, //tr11
5,11,9, //tr12
//right side
2,8,4, //tr13
4,8,10, //tr14
4,10,5, //tr15
5,10,11, //tr16
//bottom side
0,6,1, //tr17
1,6,7, //tr18
1,7,2, //tr19
2,7,8, //tr20
];
Теперь результат ожидаемый:

Отражения от направленного света
Попробуем не делать нормализацию вектора направления света, тогда значения влияют на близость источника:
//vec3 directionalLightPosition = normalize( vec3(10.0, 10.0, 5.0) );
vec3 directionalLightPosition = vec3(10.0, 10.0, 5.0);

Без нормализации вектора направления света
Точечный свет (ТС)
Чтобы преобразовать НС в ТС нужно подсчитать направления от ТС к каждой точке объекта. В вершинном шейдере добавим такой расчет:
//Point.
vec3 pointLightPosition = vec3(1.0,2.0,-1.0);
//1st
vec3 pointLightDirection = normalize( vec3(pointLightPosition.xyz - aVertexPosition09pr.xyz));
//2nd
vec3 L = vec3(uPMatrix09pr * uMVMatrix09pr * vec4(pointLightDirection, 1.0));
//3rd
vec3 N = uConvertNormalMatrix09pr * aVertexNormal09pr;
//4th
float diffuseLightAmountPoint = max( dot(normalize(N), normalize(L)), 0.0);
…
//4 variant - Ambient + Point.
vLight09pr = ambientLight + (diffuseLightAmountPoint * aVertexColor09pr);
В результате более плавный градиентный свет на объекте:

Отражение в точечном свете
Свет и текстура
Наконец, попробуем добавить к текстуре наше новое освещение с РО от ТС. В вершинном шейдере сделаем однотонный свет vec3 (.8,.8,.8) вместо красного:
//5 variant - Ambient + Point + gray light for Texture.
vLight09pr = ambientLight + (diffuseLightAmountPoint * vec3(.8,.8,.8));
А в пиксельном шейдере смешиваем цвет текстур и цвет освещения:
if(uDoTexturing09pr == 1)
{
…
highp vec4 textureColor = mix(tileColor, logoColor, logoColor.a);
gl_FragColor = vec4(textureColor.xyz * vLight09pr, textureColor.a);
}

Текстура в точечном свете
Наша модель освещения далека от совершенства и реалистичности. Можно еще добавить зеркальное отражение (ЗО), световую модель (например Phong), интерполяцию значений нормалей, прозрачность, туман, тени… Но это уже “красивости”, которые можно рассмотреть в свободное время. А так, можно уже с нашими знаниями воплощать в жизнь простые проекты в мире 3D!
 CogITas
CogITas 