Пиксель и тексель в поисках вокселя
Андрей Свирский - 25-03-2017
Строим 3D проекты – Шаг 6

Угадай материал по текстуре
В программе 2-го шага, мы нарисовали простейшую 2D фигуру. На 3-ем шаге, мы закрашивали ее разными цветами:

Заполнение цветом
Теперь разберемся, как закрасить фигуру текстурой из графического файла.
Пример на основе простейшей 2D фигуры
- Выбираем файл с изображением, которое мы наложим на наш объект-треугольник в качестве текстуры. Например, используем любой файл размером 128×128 пикселей:
Пиксели и тексель
Это изображение из 128 на 128 пикселей будет минимальным элементом текстуры — текселем (texture element). Координатные оси размещения текселей задаются буквами {s,t,p,q}. Это стандартные буквы, как и {x,y,z,w} для координат, и буквы {r,g,b,a} для цветов.
Для 2D наложения текстуры используются первые координаты (s,t).
Если тексель размером от 0 до 1, то, в данном случае, 0,5 текселей это 64 пикселей.
2. Заводим глобальные переменные для хранения изображения и текстуры:
var texture06pr = null;
var textureImage06pr = null;
3. Дополним вершинный и пиксельный шейдеры для работы с текстурой. Все, что косалось работы с цветом, можно пока удалить. В вершинный шейдер будем передавать координаты текстур:
<script id= "shader-vs06pr" type= "x-shader/x-vertex">
attribute vec3 aVertexPosition06pr;
varying highp vec2 vTextureCoord06pr;
void main(void)
{
gl_Position = vec4( aVertexPosition06pr, 1.0);
vTextureCoord06pr = (aVertexPosition06pr.xy + 0.5);
}
</script>
Для данного примера, с целью упрощения программы, для задания координат текстуры (s,t) используем координаты вершин (x,y) из aVertexPosition. Напомню, что координаты вершин у нас от -0.5 до 0.5:
var triangleVertices =
[
//Triangle's points coodinates.
-0.5, 0.5, 0.0,
0.0, 0.0, 0.0,
-0.5, -0.5, 0.0
];
поэтому, чтобы текстура выводилась из одного текселя, а не из отрицательных текселей, мы добавили к каждому значению 0.5:
vTextureCoord06pr = ( aVertexPosition06pr.xy + 0.5);
В пиксельном шейдере принимаем это значение и отправляем в функцию texture2D:
<script id= "shader-fs06pr" type= "x-shader/x-fragment">
varying highp vec2 vTextureCoord06pr;
uniform sampler2D uSampler06pr;
void main(void)
{
//gl_FragColor = vec4(1.0, 1.0, 1.0, 1.0);
gl_FragColor = texture2D( uSampler06pr, vec2( vTextureCoord06pr.s, vTextureCoord06pr.t ) );
}
</script>
4. В главный алгоритм программы добавляем функцию loadTexture () для загрузки текстуры из файла. Также добавляем обработчик события textureImage.onload, который в случае успешной загрузки изображения запускает функцию настройки текстуры и функции прорисовки:
if(gl06pr)
{
initShaders06pr(); //[1]
setupBuffers06pr(); //[2]
loadTexture06pr();
textureImage06pr.onload = function()
{
setupTexture06pr();
setupWebGL06pr(); //[3]
drawScene06pr(); //[4]
}
}
5. Добавляем описанные выше новые функции:
function loadTexture06pr()
{
textureImage06pr = new Image();
textureImage06pr.src = "textures/face-128x128.png";
}
Мы использовали HTML объект Image ().
Важно: чтобы загрузился файл текстуры, необходимо запускать программу на веб-сервере (JS не разрешено работать с файлами на компьютере пользователя). То есть, в браузере необходимо ввести адрес программы типа:
http://192.168.137.1/as/06-triangle-2d-texture
Если в указанной таким образом папке есть файл index.html с нашей программой, то он запустится автоматически. Как установить веб-сервер, написано в статье про XAMMP.
Теперь, наконец, главные действия в этой программе — устанавливаем текстуру:
function setupTexture06pr()
{
texture06pr = gl06pr.createTexture();
gl06pr.bindTexture( gl06pr.TEXTURE_2D, texture06pr);
if( !gl06pr.isTexture( texture06pr) )
console.error( "Error: Texture is invalid");
else
{
gl06pr.pixelStorei( gl06pr.UNPACK_FLIP_Y_WEBGL, true);
gl06pr.texParameteri( gl06pr.TEXTURE_2D, gl06pr.TEXTURE_MAG_FILTER, gl06pr.NEAREST);
gl06pr.texParameteri( gl06pr.TEXTURE_2D, gl06pr.TEXTURE_MIN_FILTER, gl06pr.NEAREST);
gl06pr.texImage2D( gl06pr.TEXTURE_2D, 0, gl06pr.RGBA, gl06pr.RGBA, gl06pr.UNSIGNED_BYTE, textureImage06pr );
glProgram06pr.samplerUniform = gl06pr.getUniformLocation( glProgram06pr, "uSampler06pr");
gl06pr.uniform1i( glProgram06pr.samplerUniform, 0);
}
}
а – Мы создаем объект текстуры типа WebGLTextureObject в переменной texture.
б – Связываем с программой текстуру texture в режиме gl.TEXTURE_2D.
в – Функция gl.pixelStorei () указывает WebGL как хранить данные. В данном случае, инвертирует порядок вывода текселей по оси T (они изначально идут сверху вниз).
г – Функции gl.texParameteri () указывают WebGL как выполнять сглаживание и заполнение текстурой. Об этом в другой раз.
д – Вызываем gl.texImage2D () для установки textureImage.
Посылаем загруженную текстуру в программу шейдеров.
е – Находим в шейдерах униформу uSampler и связываем ее с glProgram.samplerUniform.
ё – Устанавливаем в glProgram.samplerUniform текущую текстуру. Параметр ноль «0» соответствует текущей текстуре «TEXTURE0».
Результат программы – наложение текстуры на объект:

Объект текстурирован
Что мы видим в результате? Бесконечная поверхность текстуры виртуально формируется в 2D таким образом:
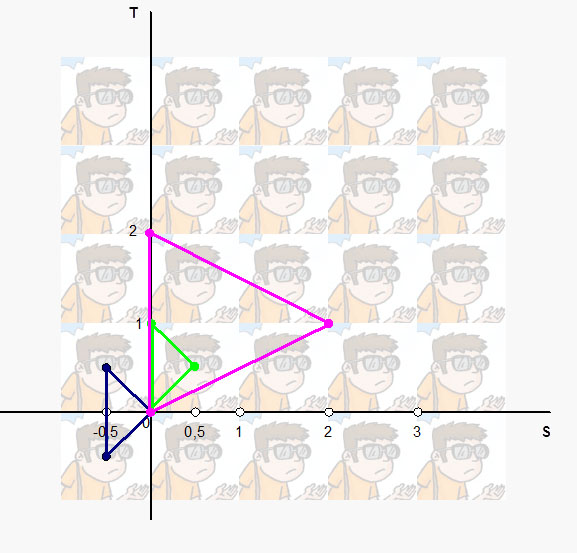
Карта текселей текстуры
Мы наложили текстуру с добавлением 0,5 к каждой координате (зеленый треугольник), чтобы использовать целый тексель, а не части с отрицательных. С исходными координатами, мы бы увидели то, что внутри синего треугольника.
Что произойдет, если размер фигуры будет больше 1×1, то есть больше текселя? Увеличим фигуру:
var triangleVertices =
[
//Triangle's points coodinates.
-1.0, 1.0, 0.0,
1.0, 0.0, 0.0,
-1.0, -1.0, 0.0,
];
В шейдере сместим координаты в положительную область:
vTextureCoord06pr = aVertexPosition06pr.xy + 1.0;

Треугольник больше текселя
В результате, фигура заполняется несколькими текселями. Заполнение будет как у розового треугольника на рисунке ранее.
При размере canvas 800×600 заметны искажения — тексели не квадратной формы. На рисунке выше, мы установили размер canvas не 800×600, а 600×600. Искажения пропали, значит, изменение размеров холста деформирует изображение.
Можно эмулировать изменение размера фигуры, умножением размера текселей, то есть, уменьшая размер текселя:
vTextureCoord06pr = (aVertexPosition06pr.xy + 1.0)*4.0;

Треугольник побольше
Конечно, такое большое и нетипичное для текстуры изображение было выбрано для большей наглядности процесса наложения текстуры. Если бы мы выбрали файл вроде такого:

Текстура кладки
то результат был бы без очевидной структуры расположения текселей текстуры:

Реальная текстура
На следующем шаге мы аналогичным образом попробуем наложить текстуру на объемную фигуру 3D.
 CogITas
CogITas